En una de mis publicaciones hablé sobre la importancia de establecer buenas bases en tu camino como programador. Entre algunos de los conceptos que mencioné, estaba el de los algoritmos. Comprender qué es un algoritmo y cómo funcionan algunos de los algoritmos más utilizados en el desarrollo de software es un tópico que considero fundamental para ser un excelente developer. Pero empecemos por lo básico: ¿qué es un algoritmo?

Un algoritmo es un conjunto ordenado y finito de operaciones que permite hallar la solución de un problema. Está definido por instrucciones o reglas bien definidas, ordenadas y finitas que permiten realizar una actividad. Dado un estado inicial, una entrada y una secuencia de pasos sucesivos, se llega a un estado final y se obtiene una solución.

Para programar de forma eficaz es necesario aprender a resolver problemas de una forma sistemática y rigurosa. Solo se puede llegar a realizar un buen programa si previamente se ha diseñado un algoritmo. Un algoritmo dará lugar a un programa que puede codificarse en cualquier lenguaje de programación.

En la mayoría de casos, hay varias formas o caminos para llegar a una solución o soluciones concretas. Sin embargo, no todas los caminos serán igual de eficientes. No es lo mismo irse de vacaciones en micro que en coche o en avión, aunque el destino sea el mismo. Por eso es importante medir la eficiencia que tiene un determinado algoritmo. Para este propósito, se idearon distintas maneras de medir dicha eficiencia teniendo en cuenta algunos casos comunes. Estas maneras son conocidas como notaciones.

Dentro de las notaciones existentes, existe una en particular de la que quiero hablar. Estoy seguro de que te habrás topado con el siguiente término en algún momento, pero, si no es así, te lo presento y haré mi mejor esfuerzo en explicártelo lo mejor que pueda en base a lo que llevo estudiado del tema. Estoy hablando de, nada más ni nada menos, que el Big O.

Este artículo es una recopilación de otros artículos un poco más complejos que he encontrado en internet, cuyos enlaces te dejo al final del artículo. También tomé prestadas algunas explicaciones y un ejemplo (que podrás leer más adelante) de este genial curso publicado en Udemy que recomiendo ampliamente.

El Big O es una métrica utilizada en la Ingeniería de Software para determinar el nivel de eficiencia y complejidad (tanto espacial como temporal) que tendrá un algoritmo bajo altas cargas de trabajo.

La eficiencia de un algoritmo vendrá dada por su tiempo de ejecución asintótico. La notación asintótica (que viene de asíntota, definida como «Una curva que se acerca indefinidamente a una recta o a otra curva sin llegar nunca a encontrarla» ), es una forma de describir una curva matemática, una forma de evolución de un fenómeno respecto a cambios en sus factores de entrada. Las notaciones asintóticas son lenguajes que nos permiten analizar el tiempo de ejecución de un algoritmo identificando su comportamiento si el tamaño de entrada para el algoritmo aumenta. Esto también se conoce como la tasa de crecimiento de un algoritmo.

De las distintas anotaciones existentes, el Big O (o también llamado Notación O) es una notación asintótica que permite analizar un algoritmo por su peor caso. Esto permite describir el crecimiento de los requerimientos de recursos (ciclos de procesamiento, tiempo, memoria, almacenamiento) de un algoritmo respecto del tamaño de los datos de entrada, o más explicitamente, respecto del tamaño del trabajo a procesar.

Sin embargo, el tiempo no es el único factor importante. Se debe tener en cuenta su complejidad espacial, o dicho de otro modo, la cantidad de memoria utilizada por el algoritmo. Normalmente se hacen compromisos entre la complejidad temporal y espacial, ya que la mejora en una vendrá en detrimento de la otra. El objetivo es encontrar un buen balance entre ambas complejidades, dadas nuestras condiciones.

Es importante tener en cuenta que el número de instrucciones u operaciones a realizar sobre los distintos inputs (entradas) no influye sobre la complejidad algorítmica. De nuevo, la complejidad algorítmica mide la forma en la que crece el tiempo de ejecución de un algoritmo según los valores de entrada.

Dado que el tiempo y ejecución de un algoritmo en base a su tamaño de entrada dependen de muchas variables (como por ejemplo, el tipo de hardware utilizado para ejecutar dicho algoritmo), es casi imposible definir un tiempo o espacio específicos. La notación asintótica permite describir cómo crecerán esos requerimientos de espacio y tiempo con respecto al tamaño de entrada recibida. Para esto, se han definido varios tipos de “órdenes” que describen las formas de crecimiento más comunes. Estos son:

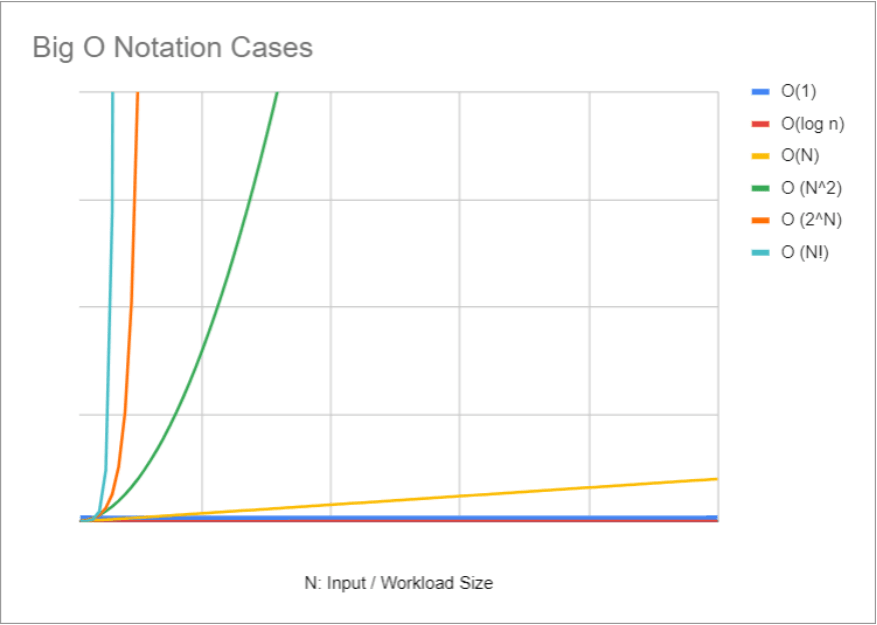
El siguiente gráfico muestra los distintos tiempos de ejecución (eje Y) de algunos de los órdenes u expresiones más comunes conforme crece el tamaño de la entrada o carga de trabajo (eje X). Como se puede ver, las expresiones O(1) y O(log n) mantienen un tiempo de ejecución y una demanda de requerimientos (operaciones u espacio) constantes a medida que crece la entrada. En cambio, otros órdenes, como O(N^2) u O(N!) muestran un tiempo de ejecución y una demanda de requerimientos mucho más elevados con respecto al tamaño de entrada.

O(1) - Orden constante: esta expresión es utilizada para describir aquellos algoritmos cuyos requerimientos de espacio o tiempo son los mismos independientemente del tamaño de entrada. Una función que sólo devuelve el primer elemento de un array (arreglo) es un ejemplo de esto. No importa el tamaño del array, la función se ejecutará en un tiempo constante (a mayor o menor medida).

O(N) - Orden lineal o Primer Orden: los algoritmos descritos con esta expresión son aquellos que presentan una complejidad algorítmica donde los requerimientos de espacio o tiempo crecen de manera proporcional a la especificación de entrada. Dicho de otro modo, a mayor tamaño de entrada, mayor tiempo de ejecución. Un algoritmo que siempre ejecuta la misma cantidad de operaciones por cada elemento de la entrada es un ejemplo de esta expresión.

O(log n) - Orden logarítmico: la principal característica de los algoritmos descritos por esta expresión es que el crecimiento de los recursos requeridos tiende a disminuir y el tiempo de ejecución se vuelve constante conforme crece el tamaño de entrada o carga de trabajo. En otras palabras, el tiempo de ejecución es más elevado para entradas pequeñas pero más óptimo para entradas extremadamente grandes.

Un gran recurso para integrar un conocimiento nuevo es el ejemplo o ilustración. Y mucho mejor si este ejemplo está relacionado con un tema que nos guste. Acá voy a dar un salto de fe y arriesgar a decir que, si te gusta programar, muy probablemente te gusten los videojuegos también 🎮

Imaginemos que tenemos una consola de videojuegos (PlayStation, Xbox, la que prefieras). Como es obvio, para disfrutar de esta consola necesitamos lo más importante: los juegos. Tenemos dos opciones para conseguirlos. Una de estas opciones es comprar y descargar los juegos mediante la tienda de la consola. La otra opción es comprarlos a través de una tienda online en formato físico y que nos los envíen a nuestra casa. ¿Cuál es la mejor opción?

La descarga nos permite tener un juego en pocas horas, dependiendo de nuestra velocidad de internet. En cambio, el envío a domicilio de un juego físico tarda uno o más días. Si queremos tener un juego solo o unos pocos, la primera opción nos sería más conveniente ya que tardaríamos menos. Pero, ¿qué sucede si queremos tener muchos juegos? La descarga total de todos esos juegos tomaría más que solo un par de horas, puede que incluso días. Esto no afecta a la entrega a domicilio, ya que si encargamos un juego, o 10, o 20, el tiempo de entrega sigue siendo el mismo.

Ahora, pensemos cada opción como un algoritmo distinto y apliquemos la notación asintótica Big O para determinar la complejidad de cada uno. Como vimos, la complejidad algorítmica mide el tiempo de ejecución según el tamaño de entrada. En este ejemplo, la cantidad de juegos a obtener es el tamaño de entrada. A más juegos (más entrada), el tiempo que tardemos en obtenerlos todos (tiempo de ejecución) se verá impactado, o no.

Tal como hemos analizado, una de las opciones (la descarga) nos da un tiempo de ejecución rápido si el tamaño de entrada (cantidad de juegos) es bajo, pero conforme la entrada vaya creciendo (osea, si queremos más juegos), el tiempo de ejecución se elevará. Estamos ante un órden de tipo lineal o también llamado O(N), siendo N la cantidad de juegos que queramos obtener.

La segunda opción (la entrega a domicilio) nos da un tiempo de ejecución constante ya que el tiempo que tarde el juego o los juegos en llegar a nuestro domicilio es el mismo (determinado por el vendedor o tienda, obviamente). Si el tamaño de entrada (los juegos) aumenta, el tiempo de ejecución sigue siendo el mismo, por lo que nos encontramos ante un órden de tipo constante o también conocido como O(1).

El Big O es una forma de analizar como crecerá la complejidad temporal y espacial de nuestro algoritmo en los extremos o peores casos. Recordá que un algoritmo de mayor complejidad puede ser más rápido que otro algoritmo de menor complejidad para rangos de entrada específicamente bajos. Sin embargo, para un N bajo todos los algoritmos van a ser rápidos. Lo importante es ver cómo se comportan cuando N crece.

La notación asintótica es un tema complejo que es difícil de cubrir en una sola publicación. No te frustres si no lo entendés de entrada. Lleva tiempo y lo importante es comprenderlo paso a paso. Sin embargo, aprender sobre este tópico es fundamental para establecer una buena base teórica que te permita elaborar algoritmos de la manera más eficiente posible. O en caso de que hayas escrito algoritmos antes de aprender sobre este tema, este conocimiento te permitirá optimizarlos. Espero que este artículo te haya permitido comprender algunos conceptos básicos y ¡te haya despertado la curiosidad por aprender más!

Y DE YAPA (en español argentino, "yapa" significa algo así como un bonus, un agregado), te comparto este mismo artículo en formato plantilla de Notion. Si utilizas esta herramienta, seguro te viene útil, ya que vas a poder editarla y añadir tus propias investigaciones sobre este tema y repasarla cuando lo necesites. Una vez abras el enlace, recordá duplicarlo en tu espacio de trabajo al clickear sobre el botón "Duplicar" (ubicado en la esquina superior derecha).